Band-Limited Signal Reconstruction from Irregular Samples with Variable Apertures
Prof. David G. Long
Brigham Young University Center for Remote Sensing
Microwave Earth Remote Sensing (MERS) Laboratory
450 Engineering Building, Provo, Utah USA
long@ee.byu.edu
|
 |
 |
Web pages and software to accompany the paper:
D.G. Long and R.O.W. Franz, Band-Limited Signal Reconstruction from Irregular Samples with Variable Apertures, IEEE Transactions on Geoscience and Remote Sensing, Vol. 54, No. 4, pp. 2424-2436, doi:10.1109/TGARS.215.2501366, 2016.
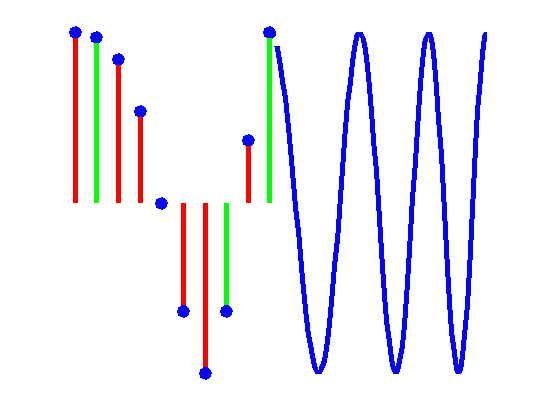
One- and two-dimensional signal reconstruction from irregularly spaced samples using (possibly) variable apertures.
Reconstruction of a band-limited signal from uniformly spaced samples
('regular sampling') is a well-understood problem treated in signal
processing textbooks: given uniformly spaced samples of the signal,
the original band-limited signal can be exactly reconstructed from the
samples by sinc interpolation so long as the signal is sampled at
twice the highest frequency of the signal, i.e., so as long as the
sampling meets the Nyquist criterion.
What happens when the sampling is irregular, i.e., not evenly-spaced? Can the original signal be reconstructed? Yes, if the δ-density of sampling meets Gröchenig's criteria (Gröchenig, 1992). Efficient numerical reconstruction algorithms have been developed to compute the reconstructed signal for the one-dimensionala signal case (Feichtinger et al., 1995).
Since sampling implies the signal needs to be bandlimited, and in practice, only a finite number of samples are available Long and Franz (2016) argue that in practice we need only consider the case of periodic functions, where periodicity is imposed by extension if required. Thus, in practice the sampling/reconstruction problem is equivalent to reconstruction of a discrete sampling of a discrete periodic signal (Gröchenig, 1993).
In practice, the sample values consist of weighted local averages of the function of interest over an effective aperture. The aperture function (also known as the impulse response or the sampling window) acts a smoothing filter and the samples can be viewed as samples of the aperture function-filtered signal. If the aperture function is fixed (i.e., the aperture function is the same for all meaurements or samples), so long as the freqeuency response of the aperture function has no nulls with in the region of support of the frequency spectrum of the signal, the effective aperture can be removed by first reconstructing the aperture-filtered signal and then deconvolving the aperture function in order to estimate the original signal.
What happens when multiple different aperture functions are used, i.e., the aperture functions are different for each sample? A solution for this case has not been previously developed.
Long and Franz (2016) derive the reconstruction equation for the general discrete periodic signal including variable apertures. For a one-dimensional M-bandlimited signal (which requires 2M+1 Fourier coefficients), a minimum of 2M+1 samples are required to fully reconstruct the signal. These samples can occur anywhere within the signal period, but must be disjoint. These samples can have different aperture functions. The signal can be exactly reconstructed so long long as the spectra of the aperture functions do not have spectral nulls within the band-limit of the signal.
In the two-dimensional case, a M1,M2-bandlimited signal can be reconstructed from (2M1+1)(2M2+1) disjoint samples, which can have differerent apertures. So-called 'cubic lattice' 2-d samplings can always be reconstructed (Long, 2021). However, unlike the one-dimensional case where the samples can be anywhere in the period, in the two-dimensional case, the general sampling case is more restrictive and must result in a full-rank reconstruction matrix to ensure full reconstruction. Long and Franz (2016) derive the general reconstruction matrix and how to test it for reconstructability in both the ideal single aperture and variable aperture cases, see also Long (2021).
The basic theory developed in Long and Franz (2016) and Franz and Long (2021) is summarized in a pdf document. We provide Matlab software to illustrate reconstruction technique. The theory includes a discussion of the two-dimensional sampling requirements and presents examples of both full-rank and reduced-rank sampling. An illustrative example from satellite remote sensing is provided. The issue of how to use 'extra' samples is briefly considered, as well. Further analysis is provided in Long (2021).
References
Feichtinger, H.G., K. Gröchenig, and T. Strohmer, 1995. Efficient
numerical methods in non-uniform sampling theory, Numerische Mathematick, vol. 29, pp. 433-440, 1995
Gröchenig, K., 1993. A Discrete Theory of Irregular Sampling, Linear Algebra and Its Applications, vol. 193, pp. 129-150.
Gröchenig, K., 1992. Reconstruction Algorithms in Irregular Sampling,
Mathematics of Computation, vol. 59, no. 199, pp. 181-194.
D.G. Long and R.O.W. Franz, 2016. Band-Limited Signal Reconstruction from Irregular Samples with Variable Apertures, IEEE Transactions on Geoscience and Remote Sensing, Vol. 54, No. 4, pp. 2424-2436, doi:10.1109/TGARS.215.2501366, 2016.
R.O. Franz and D.G. Long, 2021. Reconstructing Signals from Aperture-Filtered Samples, The American Mathematical Monthly, pg. 1-17, doi:10.1080/00029890.2022.1993712
D.G. Long, 2021. Discrete Band-Limited Signal Reconstruction from Irregular Samples, IEEE Transactions on Geoscience and Remote Sensing, Vol. 59, Nov. 5, pp. 4033-4043, doi:10.1109/TGRS.2020.3022761
Maintained by David Long
long@ee.byu.edu
Last modified: 29 Jul 2023

